Initial Observations on the SkipJack Encryption Algorithm
| Eli Biham, Alex Biryukov, Orr Dunkelman, Eran Richardson | | Adi Shamir |
| Computer Science Dept. | | Applied Math Dept. |
| Technion | | The Weizmann Institute |
| Israel | | Israel |
June 25, 1998
(DRAFT)
This note can be found in
http://www.cs.technion.ac.il/~biham/Reports/SkipJack/
Feel free to distribute
Summary
SkipJack is the secret key encryption algorithm used by the US
government in the Clipper chip and Fortezza PC card.
It was implemented in tamper-resistant hardware and its structure had
been classified since its introduction in 1993.
On June 24th, 1998, SkipJack was unclassified, and described in the
web site of NIST.
This note summarizes our main observations, after several hours of
analysis.
Our main finding so far is that SkipJack reduced from 32 to 16 rounds
can be broken by an attack which is faster than an exhaustive search.
This is obviously a very initial result, and may indicate that
SkipJack does not have a conservative design with huge margins of safety.
In the remainder of this note we describe a simplified implementation of
SkipJack, which is faster than the original published definition.
This modified description will be the basis for the subsequent
analysis.
We then use the standard terminology of differential and
linear cryptanalysis to describe our best cryptanalytic results so far.
Efficient Implementation of SkipJack
The published description of SkipJack characterizes the rounds as
either Rule A or Rule B.
Each round is described in the form of a linear feedback shift
register with additional non linear keyed G permutation.
Rule B is basically the inverse of Rule A with minor positioning
differences.
SkipJack applies eight rounds of Rule A, followed by eight rounds of
Rule B, followed by another eight rounds of Rule A, followed by
another eight rounds of Rule B.
The Software implementation becomes simpler and more efficient if we
unroll the rounds, and keep the four elements in the shift register stationary.
In this form the code is simply a sequence of alternate G operations
and XOR operations of cyclically adjacent elements.
In this representation the main difference between Rule A and Rule B
is the direction in which the adjacent elements are XORed (left to
right or right to left).
The following figure describes this representation:
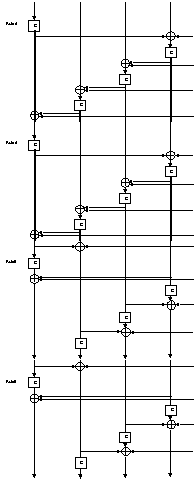
(only the first 16 rounds out of the 32 are listed).
An Observation Regarding the Key Schedule
The key schedule is cyclic in the sense that the same set of four
bytes of the subkeys (entering a single G permutation) are repeated
every five rounds, and there are only five such sets.
In addition, the key bytes are divided into two sets: the even bytes
and the odd bytes.
The even bytes always enter the even rounds of the G permutation, while the
odd bytes always enter the odd round of the G permutation.
Differential and Linear Properties of the F Table
We generated the differential and linear distribution tables of
the F Table, and found that in the difference distribution table
- The maximal entry is 12 (while the average is 1).
- 39.9% of the entries have non-zero values.
- The value 0 appears in 39360 entries, 2 in 20559, 4 in 4855, 6 in
686, 8 in 69, 10 in 5, and 12 in 2 entries.
- One-bit to one-bit differences are possible, such as 01->01 (hex) with
probability 2/256.
In the linear approximation table
- The maximal biases are 28 and -28 (i.e., 1/2+28/256 and 1/2-28/256).
- 89.3% of the entries have non-zero values.
- The value 0 appears in 7005 entries, 2 in 12456, 4 in 11244, 6 in
9799, 8 in 7882, 10 in 6032, 12 in 4354, 14 in 2813, 16 in 1814, 18 in
1041, 20 in 567, 22 in 317, 24 in 154, 26 in 54, 28 in 3.
- One-bit to one-bit linear approximations exist, such as 80->80
(hex) with probability 1/2+20/256.
Differential and Linear Properties of the G Permutation
Let a and b be two byte values such that the differences a->b and b->a
by the F Table have non-zero entries in the difference distribution table.
We can prove that the best possible characteristic of G must be of the
form:
input difference: (a,0),
output differences: (0,b),
with the intermediate differences (a,0)->(a,0)->(a,b)->(0,b)->(0,b).
There are 10778 pairs of such a and b, of which four have probability
48/2^16=2^-10.42.
They are (in hex)
- a=52, b=f5,
- a=f5, b=52,
- a=77, b=92,
- a=92, b=77.
Most others have probability 2^-14 (6672 pairs) and 2^-13 (3088
pairs), and the others are distributed with probabilities between
2^-13 and 2^-10.67.
Given a and b, there are additional characteristics with three active F
Tables (rather than only two), and for the above values of a and b
the probabilities are between 2^-15.4 and 2^-15.83.
These characteristics of G are (0,b)->(a,b) and (a,b)->(a,0).
In particular we get a cycle of three characteristics which can be
denoted in the form (a,0)->(0,b)->(a,b)->(a,0).
The linear cryptanalysis case is similar.
As the characteristics are build in a similar way where XORs are
replaced by duplication and duplication are replaced by XOR of the
subsets of parity bits, we can have the same analysis for linear
cryptanalysis.
In this case we have 52736 possible pairs of a and b, and the best
characteristic of G (a=b=60 hex) has probability 1/2+2*676/2^16=1/2+2^{-5.6}.
Differential Cryptanalysis of SkipJack with Reduced Number of Rounds
The differential cryptanalysis we describe here attacks 16-round
SkipJack considerably faster than exhaustive search.
The Characteristic
The best characteristics of 16-round SkipJack that we are aware of
at this point use the characteristics of G described above.
The plaintext difference is (a,0, a,0, 0,0, 0,b) and only six active G
permutations (in which there are a total of 14 active F Tables) are required to
achieve the ciphertext difference (0,b, 0,b, a,0, 0,0).
These characteristics have probability about 2^-72.9, and there are four
such characteristics.
The Basic Attack
Given the ciphertexts of many plaintext pairs with the difference
(a,0, a,0, 0,0, 0,b), it is easy to identify and discard most of the
wrong pairs in a 0R-attack.
However, such an attack requires about 2^73 pairs, which exceeds
the number of possible plaintext pairs.
We observe that only a 12-round characteristic is required,
with probability about 2^52.1.
In this case we choose about 2^55 chosen plaintext pairs, and can
discard most wrong pairs, except for a fraction of 2^-32 of them.
Thus, about 2^23 pairs remain.
Now we use a second observation that the same set of subkeys is used
in the first and the 16th rounds.
We try all the 2^32 possible sets of subkeys and for each remaining pair
we encrypt the first round and verify that the characteristic of G
holds, and decrypt the last round and verify whether the expected
difference (a,0) holds.
The probability that a wrong set of subkeys does not discard a pair is
2^-16*2^-10.4=2^-26.4, and thus for most sets of subkeys no pairs
remain or only one or two pairs remain.
The right set of subkeys should suggest about eight pairs, as this
is the expected number of right pairs.
Thus, we can identify 32 bits of the key, and later with similar
techniques (or even exhaustive search of the remaining 48 bits of the
key) we can complete the cryptanalysis.
We can even do moderately better using structures of several
characteristics, or using a first round trick similar to the one used
in the cryptanalysis of the full 16-round DES.
Linear Cryptanalysis of SkipJack with Reduced Number of Rounds
The linear case is very similar.
As the characteristics are built in a similar way where XORs are
replaced by duplications and duplications are replaced by XORs of the
subsets of parity bits, and as Rule A and Rule B differ essentially in
this way, we can have very similar analysis for linear cryptanalysis.
The probability of the best linear characteristic we found is about
1/2+2^-35.5, and thus the attack seems to require more known plaintexts than
possible.
However, this number can be reduced below 2^64 by using shorter characteristics.
Modified Variants of SkipJack
SkipJack uses alternately eight rounds of Rule A and eight rounds of
Rule B.
In this section we investigate whether other mixing orders
strengthen or weaken the cipher.
A simple example uses alternately four `Rule A' rounds and
four `Rule B' rounds.
We found for this cipher a 16-round characteristic with
considerably higher probability of about 2^{-52.1} rather than about 2^{-72.9}
in the case of SkipJack (this characteristic's plaintext difference is
(0,0, a,0, a,b, 0,0)).
Applying attacks similar to the ones described above should require
less than 2^30 chosen plaintexts.
When Rule A rounds and Rule B rounds appear in reverse order (i.e.,
Rule B is applied first), the results are as follows: when eight
rounds of each are applied consecutively the probability of the
characteristic reduces to 2^-77.5, and when four rounds of each are
applied consecutively, the probability increases to 2^-51.7.
This indicates that the order of Rule A and Rule B rounds can have a
major impact on the security of modified variants of SkipJack.
Other Comments on the Design
The XOR operations of Rule A and Rule B after round 8 and after round 24
(on the borders between Rule A to Rule B) are consecutive without
application of the G permutation in between.
Thus, the code
W2 = G(W2, subkey) ; from Rule A
W1 = W1 XOR W2 ; from Rule A
W2 = W2 XOR W1 ; from Rule B
W1 = G(W1, subkey) ; from Rule B
actually exchanges the words W1 and W2, and XOR only one as in
W2 = G(W2, subkey) ; from Rule A
swap W1 and W2
W1 = W1 XOR W2
W1 = G(W1, subkey) ; from Rule B
i.e., W2 becomes the previous W1.
Also, on the border between Rule B to Rule A (after round 16), there are two
applications of the G permutation on two different words, with no other linear
mixing in between.
Note that Rule A mixes the output of the G permutation to the input of the next
G permutation, while Rule B mixes the input of a G permutation to the
output of the
previous G permutation (similarly in decryption of Rule A), and thus
during encryption the Rule B rounds add little to the avalanche
effect, and during decryption Rule A rounds add little to the
avalanche effect.
It is interesting to note that (due to its design) many criteria used
in other ciphers are not used in SkipJack (for example, a difference
of one input bit in a DES S box cannot cause a difference of only one bit
in its output, but there are many such instances in
the F Table of SkipJack).
Acknowledgments
We thank Rivka Zur, the Technion CS secretary, for preparing the figures.
Back to Observations on the SkipJack Encryption Algorithm



